什么是“彩虹表”?
对于一些黑话,我本人一直是尽可能地去避免使用,而是使用一些通用的语言去概括,可当黑话达成某一个社区的共识,只要大家掌握相同的概念上下文,其实在沟通上就能很大程度地节省时间,也不会造成理解的歧义。
关于彩虹表,Wiki 的解释为:
彩虹表是一个用于加密散列函数逆运算的预先计算好的表,常用于破解加密过的密码散列。 彩虹表常常用于破解长度固定且包含的字符范围固定的密码(如信用卡、数字等)。这是以空间换时间的典型实践,比暴力破解(Brute-force attack)使用的时间更少,空间更多;但与储存密码空间中的每一个密码及其对应的哈希值(Hash)实现的查找表相比,其花费的时间更多,空间更少。使用加盐的密钥派生函数可以使这种攻击难以实现。
其实我认为我们不需要去深刻理解这个概念,只需要知道有这么一个手段的存在,因为在设计哈希摘要算法时,我们总希望尽可能地符合安全规范,因为我们总会想办法去绕过“彩虹表”的检测。
预先计算的散列链
假设我们有一个哈希方程H和一个有限的密码集合P,任意一个密码则为p,那么生成一个哈希结果的方程为:H(p) = h。如果彩虹表是一个简单的 hash 集合,那么它需要存储的空间至少为:集合P的个数 * 哈希结果h的长度,这对储存空间的要求是极高的,于是,就有人发明了散列链。
我想这里可能需要简单解释一下什么是散列链,让我们来看看 WiKi 给出的一个示例:
aaaaaa 即代表随机生成的密码,我们通过对它进行 H(Hash 算法) 得到一个值:281DAF40, 然后再对值进行一次 R(约归函数)又转化为一个特定的纯文本值:sgfnyd,因此一个简单的模式为:p1 -> h1=H(p1) -> p2=R(h1) -> h2=H(p2)...,为了节省更多的空间,因此我们会对某个密码执行多次 Hash 与约归函数,而上图中 kiebgt 就是执行两次之后得到的结果,但是不管执行多少次,我们只会在彩虹表中去存储 Head 和 Tail 节点。
或许你明白了是怎么做得,却又不知道这样做得意义,那再举一个简单的例子也许就明白了,当我们得到一串 Hash=029ECF10,首先对它进行一次约归,可得到值假如正好属于彩虹表中储存的散列链的的 Tail 值:kiebgt,那么就可以初步判断 Hash 值可能存在于散列链中,那么我们取出对应的 Head 值 aaaaaa 再进行一次散列链运算:
因此我们可以得到,哈希值 "920ECF10" 的前驱节点 "sgfnyd" 即为我们搜寻的目标密码。很神奇对吧,但这也不总是会这么顺利,有可能 R(h) 并不存在头结点的散列链中,这种情况我们就需要生成更多的散列链来继续查找。
彩虹表长什么样子
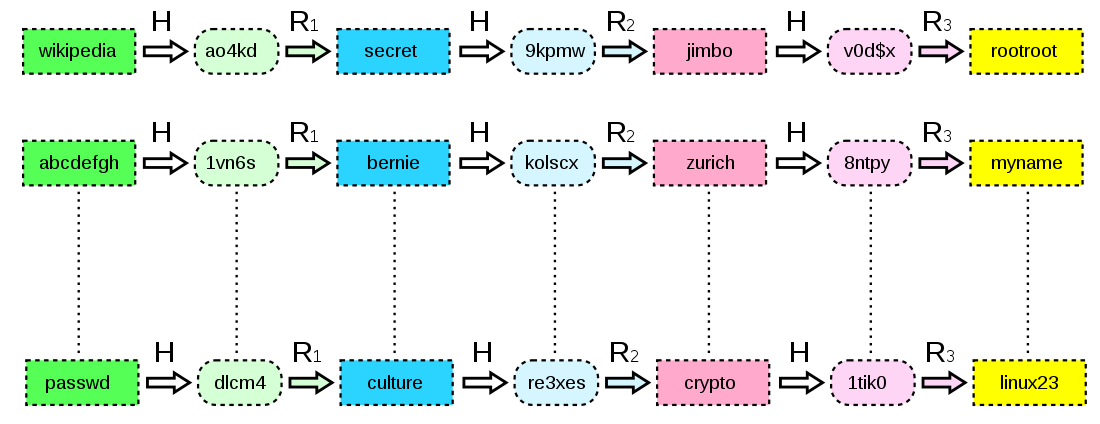
如图所示,如果看明白了这张图所代表的意义,并且明白如何根据给定的 hash 值搜索出对应的密码,那我可以默认咱们说的“彩虹表”其实是一个东西。