求质数的几种方法

今天偶然在博客上上看到有人提求质素的几种境界,在此用python进行实现代码,并进行简单的说明.

我们将要实现函数的功能是输入一个数N,能把小于N的质数个数打印出来,并计算出所耗时间.

境界1

我们采用试除法,意思就是将比N小的符合要求的每一个数都除以它,若都无法整除则N为质数,这也是我们能想到的最简单的方法,我们可以从j的范围进行优化一下,很容易想到j的范围可以取2~N/2. 代码如下:

def f1(num):
    # 2也是质数,之后程序从3开始判断
    count = 1
    for i in range(3, num):
        b = True
        for j in range(2, i/2 + 1):
            if i % j == 0:
                b = False
                break
        if b:
            count += 1
    return count

f1(100000)
# 耗时35.1589805796秒, 个数9592

境界2

我们可以从j的范围再进行优化一下,最优的范围是2~sqrt(N),这是因为因数都是成对出现,一个因子不可能超过sqrt(N).再思考一下,除了2以外所有偶数都不会是质数,因此可将偶数全部排除掉,让我们来修改并测试一下程序:

def f1(num):
    count = 1
    # 优化点1:偶数不做判断
    for i in range(3, num, 2):
        b = True
        sq = int(math.sqrt(i)) + 1
        # 优化点2:缩小试除范围
        for j in range(2, sq):
            if i % j == 0:
                b = False
                break
        if b:
            count += 1
    return count

f1(100000)
# 耗时0.264536051872秒, 个数9592

境界3

是否很有趣,通过一步一步的优化从35秒优化到了0.26秒,我们接着进行优化,普通程序员也许在境界2就浅尝辄止了,可是境界永远是用无止境的.

细想一下, 比如判断101是否为质数,sqrt(101)为10, 那我们就要依次用这个数去除以2, 3, 5, 7, 9,大家主要到其实只要除以了3以后就不用除以9了,这样我们就找到了切入点:只要尝试小于sqrt(n) 的质数即可. 顺着这个思路,我们会将求得的质数临时保存起来,于是就有了以下方法:

def f2(num):
    arrs = [2]
    count = 1
    # 质数数组中的索引
    stop = 0
    for i in range(3, num):
        k = int(math.sqrt(i))
        while stop < count and arrs[stop] <= k:
            stop += 1
        # 整除计数
        j = 0
        for k in range(stop):
            if i % arrs[j] == 0:
                break
            j += 1
        # 判定为质数后加入质数数组
        if j == stop:
            arrs.append(i)
            count += 1
    return count

f2(100000)
# 耗时0.199287338917秒, 个数9592

境界4

以上都是试除法,现在让我们来尝试以下筛法.让我们先看以下维基百科上十分形象的一张筛法工作原理图:

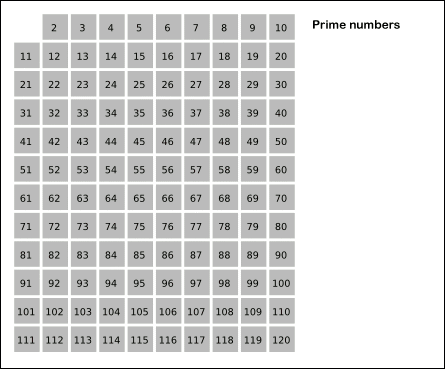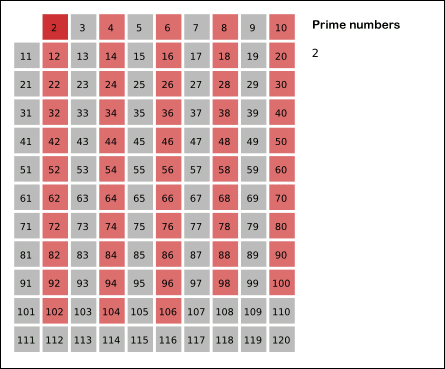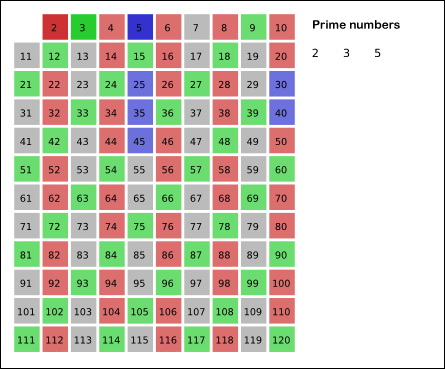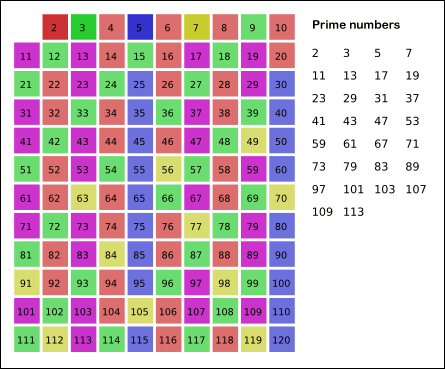
首先2是质数,因此将2的倍数全部去掉;3为质数,理应将6,9,12等去掉,同理我们只要指定一个质数范围,扩大其倍数进行筛选,将不大于N的所有倍数都筛除掉,剩下的就为质数!

我们在运用筛选法的时候,当然还是得用以上总结出来的各种技巧:

• 试除数的范围是为２～sqrt(N),同理质数求合数范围也取这个值
• 筛法的初始化数组因为要占用字节空间,应尽可能的取小.在此我们用bool型来表示,1代表质数,0代表合数,这样开销会更小
• 用加法代替乘法

def f4(num):
    # 初始化时将偶数全预筛除掉
    arrs = [0 if _i % 2 == 0 else 1 for _i in range(num + 1)]
    arrs[2] = 1
    count = 0
    for i in range(3, int(math.sqrt(num)), 2):
        if arrs[i] == 0:
            continue
        # j为i的合数,此处用加法代替乘法
        j = i + i
        while j <= num:
            arrs[j] = 0
            j += i
    # 计数
    for k in range(2, num + 1):
        if arrs[k] == 1:
            count += 1
    return count

f4(100000)
# 耗时0.03232869726秒, 个数9592

境界5

...